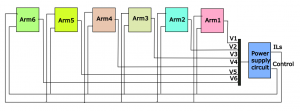
What is SimuPec®:
SimuPec® is a modeling software package specifically designed for power electronics systems within the Matlab/Simulink® Environment either for fixed admittance Simulation (using the fixed admittance Simulator SimuPec_FA®) or for non-fiixed admittance Simulation (using SimuPec®).
From the schematic diagram of the electrical circuit, SimuPec_FA® or SimuPec® automatically generate a C-language circuit description file. In the Matlab® environment you compile this C-file to generate a dll-file which can be used as an C-S-function block in the Simulink® model. This electrical circuit C-S-function block behaves exactly like any other Simulink® built-in block without interaction with SimuPec® anymore. This electrical circuit C-S-function block is very fast and reentrant (can be used more than once in the Simulink® model)
The control system of the power electronics circuit, which is normally modeled using very large number Simulink-blocks, can sometimes be the only cause of slow simulation. In this case, the whole control system “not including the power electronics system” should be converted to C-S-Function block using the Simulink-Coder Toolbox (rtw). The power electronics system is already modeled using Simupec® or SimuPec_FA® as C-S-Function block.
Simupec® and Simupec_FA® can use any of the simulation modes available from Simulink:
-
- Normalmode
- Accelaration mode
- Rapid Accelaration mode
- Rapid simulation target
They can also be used to generate C-code for any of the targets availbles from Simulink®.
Simupec_FA®
The well-known Pejovic-associated discrete circuit, fixed admittance matrix technique models the switch as an inductor during the ON-Switching state (LON=h/Gs) and as a capacitor during the OFF-Switching state (COFF=h*Gs), with h=simulation time step and Gs= fixed admittance of the switch. With a time step of 1µs, and a fixed admittance Gs=1/ohm, for example, LON is equal to 1µH and COFF is equal to 1µF, these values are not negligible and can badly affect the simulation accuracy. Using the same time step h and smaller Gs to decrease COFF will lead to increasing LON and vice versa. The only possible way to decrease both values (LON and COFF) is to use very small simulation step size h.
This simple model introduces artificial oscillations in the simulation results. For practical power electronics engineers, adding such inductances and capacitances to the power electronics circuit is not acceptable.
Many commercial real time simulators are based on this simple technique, despite its serious drawbacks, simply because it is the only fixed admittance matrix available until now.
The new proposed fixed admittance matrix technique models the switching devices i.e. IGBT/DIODE as voltage controlled resistances (German patent applied for). The resistance value in the admittance matrix is set to 1 ohm independed of device type (Diode, Thyristor, IGBT, IGBT/DIODE, etc.), switching state and device current direction, which are taken into consideration in the source/history current Vector.
The power electronics devices in the new fixed admittance matrix SimuPecFA® are modelled as piece-wise linear devices. They behave virtually as a small resistance (default value Ron=1e-3) during the turn-on switching state and large resistance (default value Roff=1e6) during the turn-off switching state. However the contribution to the admittance matrix is a fixed admittance G=1/ohm during both switching states and independent of the current direction, though different values are used in the history source current Vector.
The Figure below Shows, the fixed admittance matrix of a 2-level 3 phases DC/AC converter. The admittance of the switching device (IGBT/Diode) is set to a value of 1/ohm independent of the switching state and the current direction. The admittance of the R/L series connected load is set to 1/(R+L/h) = 0.001/ohm .
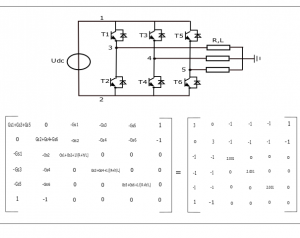
The sparse fixed admittance matrix is solved only once during the whole simulation run. During the subsequent simulation steps, the simulator needs only to multiply the history source current vector with the already solved fixed sparse LU-matrix to calculate the solution vector. The number of additions and multiplications needed for the solution vector is very small compared to the full LU-matrix solution (less than 0.3%).
Unlike the Pejovic -associated discrete circuit-technique, where a very small time step (much less than 1 micro-second) is required to get an acceptable accuracy, the new proposed fixed admittance matrix technique can work with much larger time step (some tens of micro seconds) for the same simulation accuracy.
Electrical machines can be simulated by both Simulators; the non fixed admittance simultor SimuPec® as well as the fixed admittance simultor SimuPecFA®, not only as interfacing models but also as embedded models to the whole power electronics system.
The electrical and mechanical equations of the electrical machines by the fixed admittance matrix simulation are decoupled using the values from the previous fixed Point iteration within the same time step.
The unique features of the new proposed fixed admittance matrix technique make it very suitable for large scale off-line, real time and hardware in the loop Simulation.